PAPER FUNCIONES

Descagar Paper.

INFINITOS ∞ (Georg Cantor)

   Cantor, el infinito y más allá

Mi hija Alba cuando tenía cinco años me sorprendía con afirmaciones, aparentemente trascendentes, sobre el infinito y algunas otras cuestiones peliagudas. Recuerdo que un día me dejó perplejo al soltarme a bocajarro: " Papá, el infinito nunca para, siempre se está haciendo". No sé cómo llegó a esa conclusión ni en base a qué, pero en su mente infantil parecía una evidencia pura e incontestable. Después las matemáticas no han sido, precisamente, su fuerte pero aquellas afirmaciones parecían relacionadas con las cuestiones sobre la vida, la muerte o el mundo que parecen preocupar en un momento determinado de la primera infancia a muchos niños. El post sobre los números primos, su infinitud y su "misteriosa" distribución me hizo reflexionar sobre algunos aspectos del infinito que me han hecho recordar esta anécdota y publicar este post.

En la Grecia antigua Platón, Pitágoras y Aristóles entre otros, se planteaban la existencia del infinito y las contradicciones generadas a partir de la aceptación de su existencia. Aristóteles rechazó la idea del infinito dada las contradicciones que generaba. Sin embargo, lo concibió de dos formas diferentes las cuales son las nociones que tenemos actualmente de este concepto: el infinito potencial y el infinito actual. La noción de infinito potencial se centra en la operación reiterativa e ilimitada, es decir, en la recursividad interminable, por muy grande que sea un número natural, siempre podemos concebir uno mayor, y uno mayor que este y así sucesivamente donde esta última expresión "así sucesivamente'' encierra la misma idea de reiteración ilimitada, al infinito. Por otra parte, el infinito actual se refiere al un infinito existente como un todo o unidad y no como un proceso. Kant aceptaba la posición de Aristoteles y rechazaba el infinito actual por ser imposible de ser alcanzado por la experiencia.
Georg Cantor:
El gran matemático alemán Georg Cantor dedicó gran parte de su vida al estudio del infinito, los distintos infinitos y el llamado continuo, y en el siglo XIX desarrolló la teoría de conjuntos intimamente relacionada con la teoría de números transfinitos. Cantor fundamentó una axiomática consistente que permite construir los conjuntos y posteriormente establecer el concepto de infinito. Para esto definió el concepto de "cardinalidad'' o "potencia'' de un conjunto.Dos conjuntos se dicen que tienen el mismo número de elementos, que tienen la misma cardinalidad o son equipotentes, si existe una función definida entre ellos de forma que a cada elemento de uno sólo le corresponde otro elemento del otro conjunto, y viceversa.

A partir de esta definición se puede establecer la idea de conjunto infinito. Se dice que un conjunto es infinito si existe un subconjunto con la misma cardinalidad o que es equipotente con él. Esta definición plantea una contradicción con la intuición, pues todo subconjunto como parte del conjunto total parece que deba tener menos elementos. Eso es así, efectivamente, en los conjuntos finitos, pero no en los infinitos como podemos observar con un ejemplo sencillo dentro del conjunto de los números naturales. Supongamos que al número natural 100.000.001 le hacemos corresponder el número 1, al 100.000.002 el 2, al 100.000.003 el 3 y así establecemos una correspondencia número a número tan extensa como queramos. Vemos que a cada elemento del subconjunto de números naturales que comienzan con el 100.000.001 le hacemos corresponder un número, y sólo un número del conjunto total de los números naturales, y viceversa.
Cantor se dio cuenta de que existen diferentes grados de infinitudcomparando los infinitos de los números naturales N {1,2,3,...n}, racionales Q (fracciones) y reales R(racionales + irracionales). Al cardinal infinito del conjunto de los números naturales le asignó el número llamado Aleph-0 y vio que era del mismo orden que el correspondiente a los números racionales, aunque estos son mucho más densos en la recta. Pero en el caso de los números reales su cardinal transfinito es de mayor orden pues su conjunto no es numerable (no se pueden poner en correspondencia, uno a uno, con los números naturales). A este cardinal le asignó el nombre de Aleph-1 y se supone que R es capaz de llenar la recta por completo, si se admite la hipótesis del continuo (a diferencia de lo que ocurre con los números racionales, los enteros o los naturales).
El descubrimiento de la existencia de cardinales transfinitos supuso un desafío para un espíritu tan religioso como el de Georg Cantor. Y las acusaciones de blasfemia por parte de ciertos colegas envidiosos o que no entendían su trabajo no le ayudaron. Sufrió de depresión, y fue internado repetidas veces en hospitales psiquiátricos. Su mente luchaba contra varias paradojas de la teoría de los conjuntos, que parecían invalidar toda su teoría (hacerla inconsistente o contradictoria, en el sentido de que una cierta propiedad podría ser a la vez cierta y falsa). Trató durante muchos años de probar la hipótesis del continuo, lo que se sabe hoy que es imposible, y que tiene que ser aceptada (o rehusada) como axioma adicional de la teoría, como ocurre con el llamado quinto postulado euclidiano sobre las rectas paralelas. Si se admite tenemos una geometría plana consistente, y si no se admite tenemos nuevas geometrías no planas también consistentes.
Cantor al desarrollar la que él mismo bautizó "aritmética de los números transfinitos", dotó de contenido matemático al concepto de infinito actual. Y al hacerlo así puso los cimientos de la teoría de conjuntos abstractos, contribuyendo además, de forma importante, a fundamentar el cálculo diferencial y el continuo de los números reales. El más notable logro de Cantor consistió en demostrar, con rigor matemático, que la de infinito no era una noción indiferenciada. Sus resultados fueron tan chocantes a la intuición de sus contemporáneos, que el eminente matemático francés Henri Poincaré condenó la teoría de números transfinitos como una "enfermedad", de la que algún día llegarían las matemáticas a curarse.Y Leopold Kronecker, que fue uno de los maestros de Cantor, y miembro preeminente de la matemática institucional alemana, llegó incluso a atacarle directa y personalmente, calificándolo de "charlatán científico", " renegado" y "corruptor de la juventud".
Empezó a interpretar e identificar el infinito absoluto (que no es concebible por la mente humana) con Dios, y escribió artículos religiosos sobre el tema. Murió en una clínica psiquiátrica, aquejado de una enfermedad maníaco-depresiva.Hoy en día, la comunidad matemática reconoce plenamente su trabajo, y admite que significó un salto cualitativo importante en el raciocinio lógico.

             Reflexiones:

Lo infinitamente pequeño o lo infinitamente grande, las iteraciones hasta el infinito en límites continuos o en fractales parecen conceptos ajenos a lo cotidiano, pero no es así. En las funciones continuas el cálculo infinitesimal (lo infinitamente pequeño) es una herramienta imprescindible para la ciencia y la tecnología, con ella parece que casi conseguimos tocar el propio infinito. Recuerdo la fascinación que consiguieron ejercer sobre mi mente adolescente los límites infinitos y las sumas infinitas de funciones que se aproximan a una función dada (series de Taylor), así como los cálculos de máximos y mínimos aplicados a cosas cotidianas (como el cálculo del mínimo material con el que construir un cazo de un litro de capacidad). Cuando todos estos cálculos lograban materializarse en algo concreto parecía pura magia.
Toda la revolución cuántica se basa en el cuanto de acción, la mínima acción no puede ser infinitamente pequeña o cero, como suponía la física clásica, y de esa propiedad básica emerge el mundo cuántico y toda su "magia". Por otra parte, se creía infinita la velocidad de la luz, pero de su finitud y de la constatación de que es una magnitud constante, independientemente del sistema de referencia, se ha llegado a la más bella teoría física creada por el hombre: la teoría de la relatividad. En estas dos teorías, en su necesaria conjunción descansa la esperanza de poder desentrañar los secretos más intimos de la materia y del espacio-tiempo.

CONJUNTOS

DEFINICIÓN DE CONJUNTOS 

En matemáticas, un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.Ejemplo: el conjunto de los colores del arcoíris es:AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:

P = {2, 3, 5, 7, 11, 13, ...}

Un conjunto queda definido únicamente por sus miembros y por nada más. En particular, un conjunto puede escribirse como una lista de elementos, pero cambiar el orden de dicha lista o añadir elementos repetidos no define un conjunto nuevo. Por ejemplo:


S = {Lunes, Martes, Miércoles, Jueves, Viernes}
   = {Martes, Viernes, Jueves, Lunes, Miércoles}


AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}
    = {Amarillo, Naranja, Rojo, Verde, Violeta, Añil, Azul}

Los conjuntos pueden ser finitos o infinitos. El conjunto de los números naturales es infinito, pero el conjunto de los planetas en el Sistema Solar es finito (tiene ocho elementos). Además, los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números.Los conjuntos son un concepto primitivo, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere pues la introducción de axiomas y conduce a la teoría de conjuntos.

TIPOS DE CONJUNTOS

• Notación
• Igualdad de Conjuntos
• Conjuntos Vacíos
• Subconjuntos
• Conjuntos Disjuntos
• Cardinalidad

 OPERACION CON CONJUNTOS

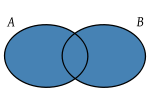
• Unión: (símbolo ∪) La unión de dos conjuntos A y B, que se representa como A ∪ B, es el conjunto de todos los elementos que pertenecen al menos a uno de los conjuntos A y B.

• Intersección: (símbolo ∩) La intersección de dos conjuntos A y B es el conjunto A ∩ B de los elementos comunes a A y B.

• Diferencia: (símbolo \) La diferencia del conjunto A con B es el conjunto A \ B que resulta de eliminar de A cualquier elemento que esté en B.

• Complemento: El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos que no pertenecen a A, respecto a un conjunto U que lo contiene.

• Diferencia simétrica: (símbolo Δ) La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.

• Producto cartesiano: (símbolo ×) El producto cartesiano de dos conjuntos A y B es el conjunto A × B de todos los pares ordenados (a, b) formados con un primer elemento a perteneciente a A, y un segundo elemento b perteneciente a B.

ÁREA

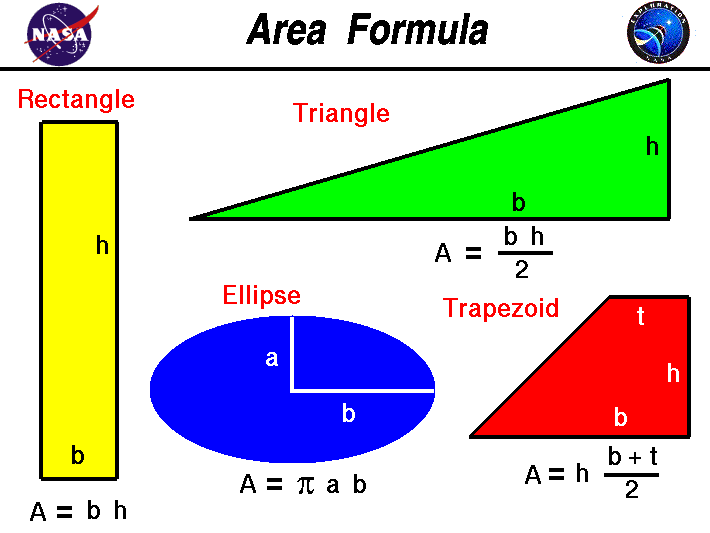
DEFINICIÓN DE ÁREA

Para superficies planas, el concepto es más intuitivo. Cualquier superficie plana de lados rectos, por ejemplo un polígono, puede triangularse y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial.Para poder definir el área de una superficie en general –que es un concepto métrico–, se tiene que haber definido un tensor métrico sobre la superficie en cuestión: cuando la superficie está dentro de un espacio euclídeo, la superficie hereda una estructura métrica natural inducida por la métrica euclidiana.El área es una medida de extensión de una superficie, expresada en unidades de medida denominadas unidades de superficie. El área es un concepto métrico que requiere que el espacio donde se define o especifique una medida. 

NÚMEROS

DEFINICIÓN DE NÚMEROS

Del latín numĕrus, el término número se refiere a la expresión de una cantidad con relación a su unidad. Se trata, por lo tanto, de un signo o un conjunto de signos. Uno (1), dos (2), tres (3), cuatro (4), cinco (5), seis (6), siete (7), ocho (8), nueve (9) y cero (0) son los números naturales. De todas formas, cabe destacar que algunos matemáticos no consideran al cero entre los números naturales. 

El conjunto de los números enteros está formado por los números naturales y los números negativos (-1, -2, -3...). La teoría de los números reconoce otras clasificaciones, como los números primos (el número natural que tiene solo dos divisores: él mismo y el uno) y los números racionales (que pueden representarse como el cociente de dos enteros que tienen denominador distinto de cero). 

Además de todo esto nos encontramos con otra amplia variedad de números. Así, también podemos referirnos a los conocidos como números romanos que son aquellos que dan forma al sistema de numeración creado durante la Antigua Roma y que concretamente son letras en mayúsculas que representan las distintas cantidades.
De esta manera, por ejemplo, la V equivale al número 5, la L corresponde al 50, la D tiene un valor de 500, la M es igual a 1000 y la X se corresponde al 10.
De la misma forma, tampoco podemos pasar por alto la existencia de los conocidos como números ordinales que son los que se emplean para establecer un conjunto bien ordenado, para darle un orden a una secuencia concreta. De esta manera, tendríamos: primero, segundo, tercero, cuarto…
Frente a estos últimos están los conocidos como números cardinales que son los que se usan básicamente para contar. Entre ellos están el 1, el 2, el 3, el 4…
Además de todos estos citados números también podemos hablar de los números arábigos, que son los que pertenecen al sistema de numeración arábiga, o de los números fraccionados que son aquellos que identificamos como quebrados. Un ejemplo de este último caso sería 2/3.
A todo ello tendríamos que añadir el hecho de que existen una serie de números que se consideran que tienen misterios encerrados o que están relacionados con un elemento muy concreto. De esta manera, por ejemplo, el 666 se asocia a Satanás, tal y como queda patente en el Apocalipsis del Nuevo Testamento.
Por otra parte, se conoce como número a una cantidad de personas o cosas (“Los espectadores se acercaron en gran número”); a las ediciones sucesivas de una publicación periódica (“El próximo número de la revista tendrá 150 páginas”); y a las partes o actos de un espectáculo (“El número del payaso fue el más divertido”).
También se conoce como número al billete de lotería o de una rifa: “Si sale sorteado mi número, me compro un coche nuevo”.
Por último, cabe destacar que Números es un libro de la Biblia que forma parte del Antiguo Testamento, entre Levítico y Deuteronomio. Al pertenecer al Pentateuco, Números es atribuido a Moisés y se supone que ha sido escrito cerca del año 1.300 a.C.

Enumeración de los tipos 

La teoría de los números trata básicamente de las propiedades de los números naturales y los enteros, mientras que las operaciones del álgebra y el cálculo permiten definir la mayor parte de los sistemas numéricos, entre los cuales están:

• Números naturales
• Número primo
• Números compuestos
• Números perfectos
• Números enteros
• Números negativos
• Números pares
• Números impares
• Números racionales
• Números reales
• Números irracionales
• Números algebraicos
• Números trascendentes:
• π
• e
• Extensiones de los números reales
• Números complejos
• Números hipercomplejos
• Números Cuaterniones
• Números Octoniones
• Números hiperreales
• Números superreales
• Números surreales
• Números usados en teoría de conjuntos
• Números ordinales
• Números cardinales
• Números transfinitos